Rôzni hráči pristupujú k licitácii rôzne, hlavne v zásahoch. O hráčoch, ktorí intenzívnejšie zasahujú do dražby, či ju ženú na vyššie stupne sa zvykne hovoriť, že sú agresívni.
Dá sa táto agresívnosť nejako merať?
Možno zaviesť niekoľko mier agresívnosti páru.
1. Ako často pár zohráva?
Zo štatistického hľadiska by mal každý pár zohrávať približne polovicu z odohraných rozdaní, ak ignorujeme odpasované rozdania. Pár, ktorý zohráva výrazne častejšie môžeme označiť za agresívnejší, než pár, ktorý zohráva menej často.
Nedostatkom tejto miery je, že nezohľadňuje vlastnosti rozdaní, v ktorých pár nechal či nenechal zohrávať súperov.
1.1 Porovnanie, či páry na tej istej linke zohrávali alebo nezohrávali
Vyššie uvedená upravená miera. Ak sa na všetkých stoloch zohrávalo na tej istej linke, tak je rozdanie z hľadiska agresivity neutrálne, prípadne doplnkovou mierou je stupeň na ktorom sa hralo. Ak sa na linke zohrávalo iba raz, tak pár ktorý zohrával bol vysoko agresívny alebo súperi boli vysoko pasívni.
[latex] $a=1-\displaystyle\frac{n}{s}$ pár zohrával\\$a=\displaystyle\frac{n}{s}-1$ pár nezohrával\\
$a$ – agresivita, $n$ – koľkokrát sa na linke zohrávalo,
$s$ – počet stolov
[/latex]Agresivita páru je priemer agresivity zo všetkých párom odohraných rozdaní. Ak je rovný nule – pár nie je ani agresívny ani pasívny, ak je kladný je agresívny, ak je záporný, je pasívny. Zatiaľ ma nenapadá, akú hodnotu agresivity priradiť, ak bolo rozdanie odpasované, ale môžme sa na to dívať tak, že pár nezohrával a platí druhý vzorec.
P.S. Oba vzorce sa stanú jedným vzorcom, ak zavedieme premennú z, ktorá nadobúda hodnoty +1 a -1, pár zohrával z=+1, nezohrával z=-1
[latex]$a=z\cdot\left(1-\displaystyle\frac{n}{s}\right)$
[/latex]Na prvý pohľad táto miera vyzerá byť dobrou mierou, len by sa malo premietnuť, či nebolo ponechanie iniciatívy súperom efektívne. Ak má pár za agresivitu súperov top, tak by sa mu nemala rátať záporná agresivita. Čiže váha zápornej agresivity by s počtom získaných percent za rozdanie mala klesať a v prípade získania topu by mala byť rovná nule (ak pár dal kontru, za top by mala byť agresivita rovná +1 ?). V takom prípade však súčet priemerných agresivít nebude rovný nule, ale bude kladný.
Vzorec pre agresivitu sa potom zmení takto (bez zohľadnenia kontry)
[latex]ak $z=1, a=z\cdot\left(1-\displaystyle\frac{n}{s}\right)$\\
ak $z=-1, a=z\cdot\left(1-\displaystyle\frac{n}{s}\right)\cdot(1-p)$\\
p – percentuálna úspešnosť/100
[/latex]1. 2 So zohľadnením kontry a rekontry
[latex]ak $z=1, a=r+z\cdot\left(1-\displaystyle\frac{n}{s}\right)$\\
ak $z=-1, a=k+z\cdot\left(1-\displaystyle\frac{n}{s}\right)\cdot(1-p)$\\
r=0 – nebola rekontra, r=1 – bola rekontra
k=0 – nebola kontra, k=1 – bola kontra
[/latex]1.3 Odstránenie vlastného vplyvu
Pri takto stanovenej miere agresivity je maximum agresivity výrazne nižšie než pri veľkom počte stolov. Ak máme iba dva stoly maximum (ak neberieme do úvahy kontry je +0.5), s rastúcim počtom stolov sa v limite blíži k +1. Pokiaľ by sme však agresivitu počítali iba z výsledkov ostatných stolov, možno zaviesť takú mieru, v ktorej bude maximum agresivity vždy rovné +1 ak nebola rekontra a +2, ak bola. Takouto mierou je:
[latex]ak $z=1, a=r+z\cdot\left(1-\displaystyle\frac{n-1}{s-1}\right)$\\
ak $z=-1, a=k+z\cdot\left(1-\displaystyle\frac{n}{s-1}\right)\cdot(1-p)$\\
[/latex]2. Rozdeľme rozdania na tie v ktorých má pár:
a) prevahu bodov
b) menej bodov
c) 20 bodov
Zistíme priemernú početnosť pre 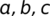 . Ak je
. Ak je  , pár je aktívny, [latex][preamble][/preamble]a<A[/latex] je pasívny.
, pár je aktívny, [latex][preamble][/preamble]a<A[/latex] je pasívny.
Ak je b>B, pár je agresívny, ak je b<B, je defenzívny.
Ak je c > 50%, pár je aktívny, ak je c<50% je pasívny.
Aj táto metóda nezohľadňuje celkom komplexné vlastnosti rozdaní. Z globálneho pohľadu už asi dostaneme signifikantné čísla, ale v konkrétnom rozdaní, možno zvolený prístup k dražbe bol správny.
3. Miera agresivity z pohľadu minimaxu
Ako často pár hrá záväzok pod minimaxom, nad minimaxom, optimálny záväzok. Ako často hrá záväzok s opačným znamienkom z pohľadu minimaxu.
Ak pár hráva často záväzky pod minimaxm, je pasívny, ak nad minimaxom je agresívny, ak hrá záväzky rovné minimaxu je aktívny.
3.1 Vyššie uvedené, ale z pohľadu úspešnosti.
4. Miera nevyrovnanosti
Často sa stáva, že pár strieda počas turnaja taktiku. Boli sme agresívni, doplatili sme na to, v nasledujúcich rozdaniach sme pasívni a znova na to doplatíme.
5. Ako často pár okontroval záväzok, z toho ako často súper splnil a ako často súper nesplnil.
Ak nesplnil možno to analyzovať z hľadiska minimaxu 1. bolo lepšie prelicitovať a splniť vlastný záväzok 2. bolo to optimálne.
V rámci páru možno zmerať mieru agresivity jeho členov tak, že sa porovná, aké sú jednotlivé uvedené miery, keď hrajú spolu a keď hrajú s inými partnermi. Pokiaľ u jedného z nich miera agresivity klesne a u druhého stúpne, tak druhý je agresívnejší, ak sa u nich pohne rovnakým smerom, tak to skôr vypovedá o miere agresivity iných partnerov.
6. Mierou agresivity by mohol byť priemerný stupeň na ktorom pár zohrával.
Nedostatkom tejto miery je, že na vyššom stupni možno pár hral, lebo ho tam súperi vytlačili, takže v jednotlivých prípadoch vyšší stupeň záväzku môže odrážať agresivitu súperov. Aj v takom prípade však čiastočne odráža aj agresivitu skúmaného páru, lebo sa nedal odstaviť od zohrávky. Na druhej strane zas, ak sme agresívne dražili a súperi boli pasívni, tak budeme zohrávať na nízkom stupni (v extrémnom prípade na prvom).
6.1 Mierou agresivity by mohol byť priemerný stupeň záväzkov bez ohľadu na to, ktorá linka ich zohrávala.
6.2 Miera agresivity páru odvíjajúca sa od priemerného stupňa na ktorom sa rozdanie zohrávalo a stupňa záväzku na ktorom pár alebo súperi zohrávali
[latex]$a=z\cdot(h-h_0)$$h$ – stupeň záväzku
$h_0$ – priemerný stupeň záväzkov rozdania[/latex]
Stupeň h nech je definovaný takto: Pas -0, stupeň záväzku+stupienok záväzku, kde =0
=0.1
=0.2
=0.3 a NT=0.4
7. Komplexná miera agresivity
Každá z navrhnutých mier má svoje výhody a nevýhody. Častosť zohrávania je odrazom agresivity páru, častosť kontrovania a rekontrovania tiež, priemerný stupeň na ktorom pár zohráva či prinúti zohrávať súperov tiež. Na druhej strane či pár bude alebo nebude zohrávať a na akom stupni sa odvíja od vlastností konkrétneho rozdania a že zohrával na vyššom stupni nemuselo byť v dôsledku vlastnej agresivity ale v dôsledku agresivity súperov. Takže miera agresivity by mala zohľadniť všetky uvedené aspekty. Komplexná miera agresivity by preto mala byť kombináciou miery 6.2 a 1.3
Hypotézy:
H1 – primálo agresívne páry budú mať horšie výsledky
H2 – mierne agresívnejšie páry bude mať lepšie výsledky
H3 – priveľmi agresívne páry budú mať horšie výsledky
H4 – páry s lepšou zohrávkou budú zohrávať záväzky na vyššom stupni
Traduje sa historka, že nejaký veľmi dobrý pár sa rozhodol odohrať celý turnaj tak, že po celý čas budú pasovať a údajne daný turnaj vyhrali, či aspoň mali nad 55%. Osobne silne pochybujem o jej pravdivosti. Za istých okolností odpasovanie rozdania v ktorom celé pole draží slem a padá prinesie úspech, ale pravdepodobnosť toho je mizivá. Pokiaĺ však viete veľmi dobre brániť, tak v odpasovaných rozdaniach určite získate viac než 0% lebo takmer vždy sa niekto nájde, kto na linke s prevahou bodov spadne či nechá hrať a plniť súperov. Ak v takýchto rozdaniach získate 30%, v rozdaniach kde majú prevahu bodov súperi by ste museli uhrať 80%, aby ste sa dostali na spomínaných 55%. Pokiaľ však budete na pasívnej linke, tak táto miera úspešnosti môže byť výrazne vyššia.
Terminologické nejasnosti
Kým v bežnej komunikácii je antonymom k agresívny – defenzívny, v bridži sa často ako antonymum k agresívny používa pasívny.
Filozofický problém – čo je prejavom väčšej agresivity – okontrovanie záväzku súperov alebo jeho prelicitovanie?
Načo je dobré takéto teoretizovanie?
Možno že nanič 🙂
Pár by mal svoju licitačnú agresivitu prispôsobiť úrovni svojich technických zručností. Pokiaľ by pár vedel vždy vylicitovať optimálne záväzky, ale zohrávka hlavného hráča by bola podpriemerná, dosahované výsledky by boli podpriemerné s občasným povyskočením na čelné umiestnenie. Na druhej strane, iba ak budete zohrávať technicky náročné splniteľné záväzky a budete ich nejakú dobu pravidelne padať, tak tú nevyhnutnú rutinu nadobudnete.
Druhou veľmi zanedbávanou vecou je partnerská spolupráca pri obrane. Ja osobne mám pri bridži najväčší pôžitok, ak si s partnerom na obrane rozumieme a poraziteľné záväzky porazíme, v neporaziteľných nezadáme nadzvih a splniteľné porazíme tiež, ak hlavný hráč urobí čo i len jedinú chybičku (aj preto celkom nerozumiem vyplakávaniu – „Celý večer som nemal body a ani raz som nezohrával“).
Primeraná miera agresivity je v bridži nevyhnutná, pokiaľ chcete útočiť na popredné miesta, premrštená agresivita však vedie ku katastrofálnym výsledkom a asi najtragickejšie je, ak táto neprimeraná agresivita zostáva v klube nepotrestaná, ale na solídne obsadenom turnaji sa nevyplatí.
Napríklad v poslednom zápase tohoročného stretnutia Košice-Miškovec sme vysoko vyhrali, aj preto, lebo naši súperi boli v licitácii pasívni – veľmi často nás nechávali zohrávať, hoci mali prevahu bodov a tuším ani raz nám nedali kontru – kontra na čiastočný záväzok je síce veľmi nebezpečná, ale niekoľkokrát sme dražili s tým, že kontra príde a ešte sa nám to oplatí, ale keďže neprišla, oplatilo sa to ešte väčšmi.
Čo je cieľom licitácie?
Možno vyčleniť tri základné ciele licitácie:
- Nájsť optimálny záväzok pre vlastnú linku
- Zamedziť nájdeniu optimálneho záväzku súperom
- Ak budeme brániť, odovzdať si počas dražby také informácie, ktoré nám pomôžu nájsť optimálny štart a optimálnu líniu obrany.
Za agresívnu dražbu sa pokladajú hlavne 2. a 3. cieľ, 1. cieľ sa agresívnou dražbou dosahuje hlavne pri podlimitných a hraničných záväzkoch.
Agresívna dražba je efektívna, ak prispeje k niektorému z uvedených cieľov a je neefektívna, ak naopak pomôže súperom niektorý z týchto cieľov dosiahnuť. Miera agresivity by nejako mala odrážať aj jej efektivitu. Agresivita sama osebe nie je ani zlá ani dobrá, ak je efektívna je pre pár dobrá, ak je neefektívna je zlá.

Komentáre